我們已經知道如何計算兩個向量之間的關聯性 α,接下來我們要將其應用到 Self-Attention 模組中,來生成最終的輸出向量 b_1。
計算 Query 和 Key
將輸入向量 a_1 乘以矩陣 W_q,得到向量 q_1,這個向量被稱為 Query,類似於搜尋引擎中的關鍵字。接著,將其他輸入向量 a_2、a_3 和 a_4 乘以矩陣 W_k,分別得到向量 k_2、k_3 和 k_4,這些向量被稱為 Key。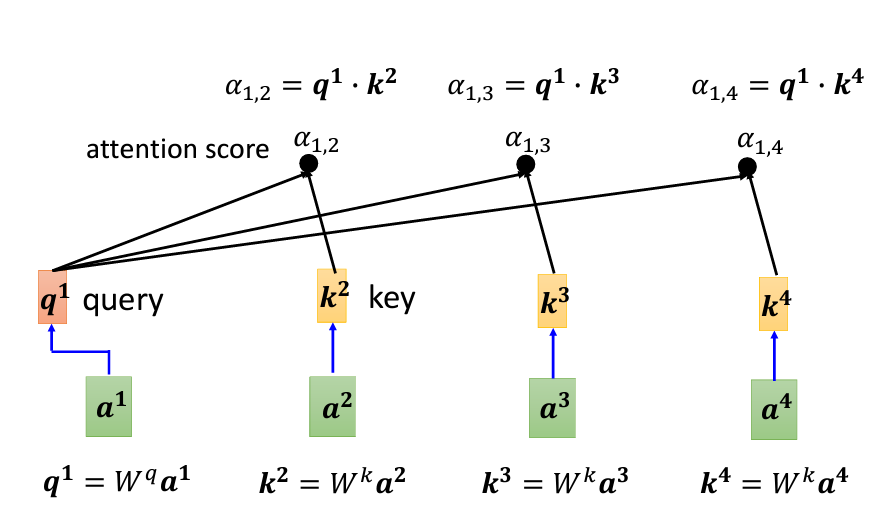
計算 Attention Score
現在,我們要計算 a_1 與 a_2、a_3、a_4 的關聯性。具體來說,通過計算 q_1 與每個 k 向量的內積(dot product),得到它們的關聯分數,也就是 Attention Score,並且用 α 來表示。比如,q_1 與 k_2 的內積結果記作 α_{1,2},表示 a_1 與 a_2 之間的關聯性。同理,計算 q_1 與 k_3 和 k_4 的內積,得到 α_{1,3} 和 α_{1,4}。此外,q_1 也會與 k_1 自己計算關聯性,這裡的結果為 α_{1,1}。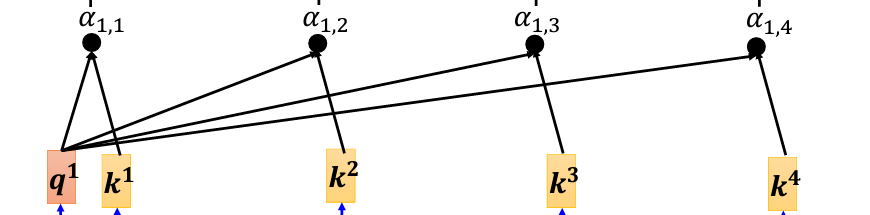
Normalization 處理
當我們得到了 α_{1,1}、α_{1,2}、α_{1,3} 和 α_{1,4} 之後,接下來使用 Softmax(或其他激活函數) 函數將它們正規化,使這些分數成為一個概率分佈,得到新的 α 值(α')。Softmax 的作用在於將原來的關聯性進行縮放和歸一化,使其更適合作為權重。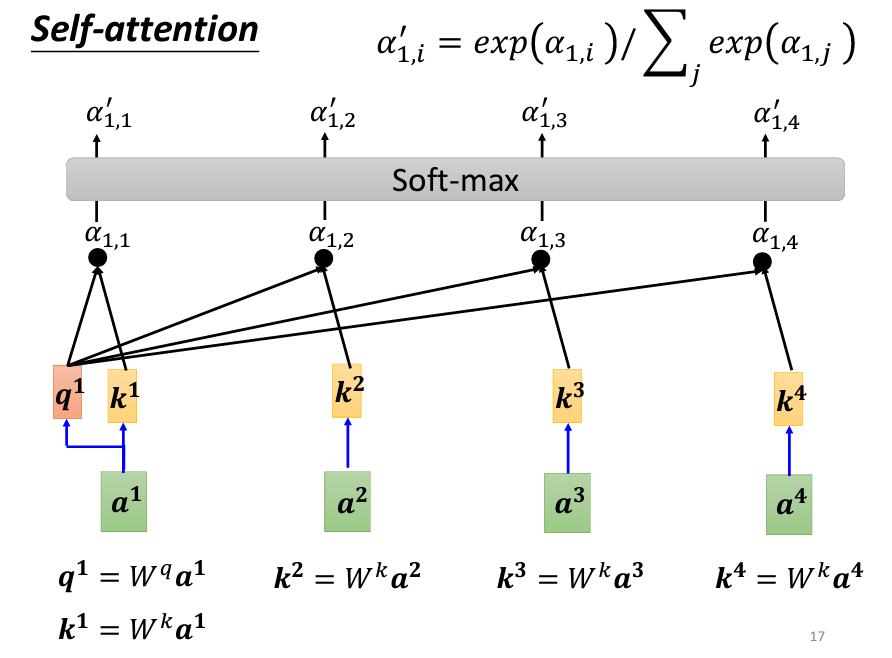
抽取重要資訊
當我們有了 α' 之後,接下來要根據這些分數來抽取序列中的重要資訊。為此,將每個輸入向量 a_1、a_2、a_3 和 a_4 乘以一個矩陣 W_v,得到新的向量 v_1、v_2、v_3 和 v_4。然後,將這些 v 向量分別與對應的 α' 相乘,再進行加權求和,最終得到 b_1。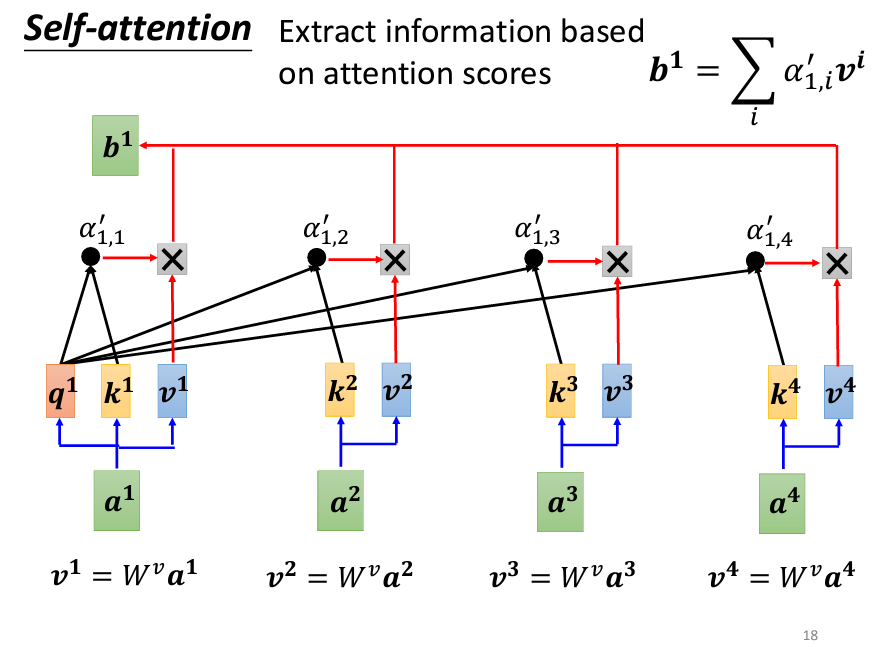
這裡的概念是,與 a_1 關聯性越強的向量,其對最終結果 b_1 的影響越大。如果 a_1 與 a_2 的關聯性很強,那麼 b_1 的值就會更接近 v_2。
生成 Q、K、V 向量:
a_i 都會生成三個不同的向量,分別是 Query q_i、Key k_i、和 Value v_i。a_1 到 a_4,通過與三個不同的參數矩陣(W_q、W_k、W_v)相乘,分別生成 Q、K、V 向量。a_1 到 a_4 組合成矩陣 I,則可以表示為: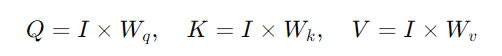
Q、K、V 矩陣的每一列(column)分別對應 q_1 到 q_4、k_1 到 k_4、v_1 到 v_4。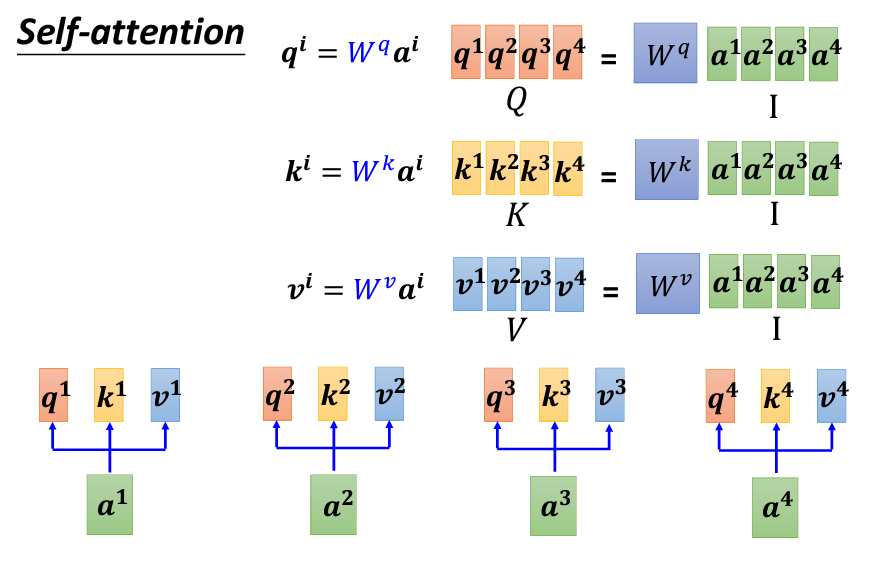
計算 Attention Scores:
q_i 都需要與每一個 Key k_j 計算內積(inner product),這可以用矩陣乘法來表示: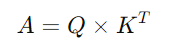
A 是一個矩陣,其每個元素 α_{i,j} 代表 q_i 與 k_j 的內積結果(即 Attention Score)。K^T 表示 K 的轉置矩陣(圖片上的K是打橫的,表示是K^T)。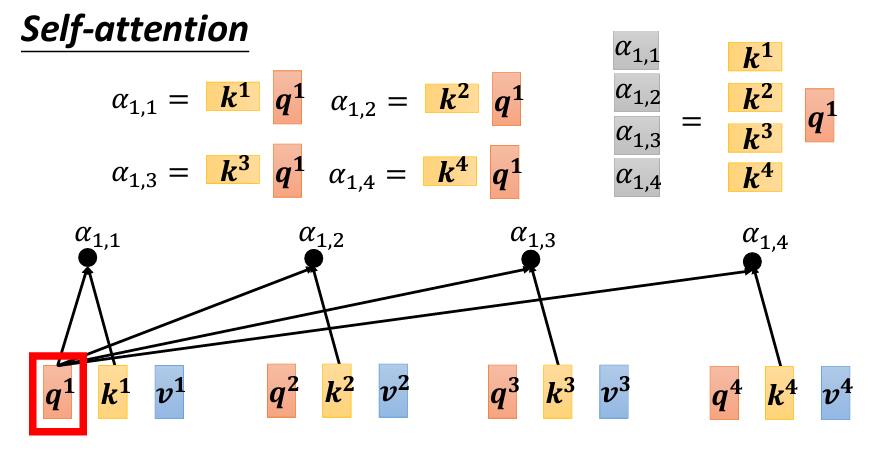
正規化:
A 會進行正規化。一般情況下會使用 Softmax 函數,對每一個 Query 所對應的列進行 Softmax 轉換,使得每一列的分數總和為 1: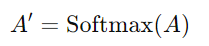

生成最終輸出:
A' 計算完成後,將其與 Value 向量矩陣 V 相乘,得到最終的輸出矩陣 O: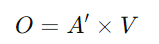
O 的每一列就是 Self-Attention 機制最終生成的輸出。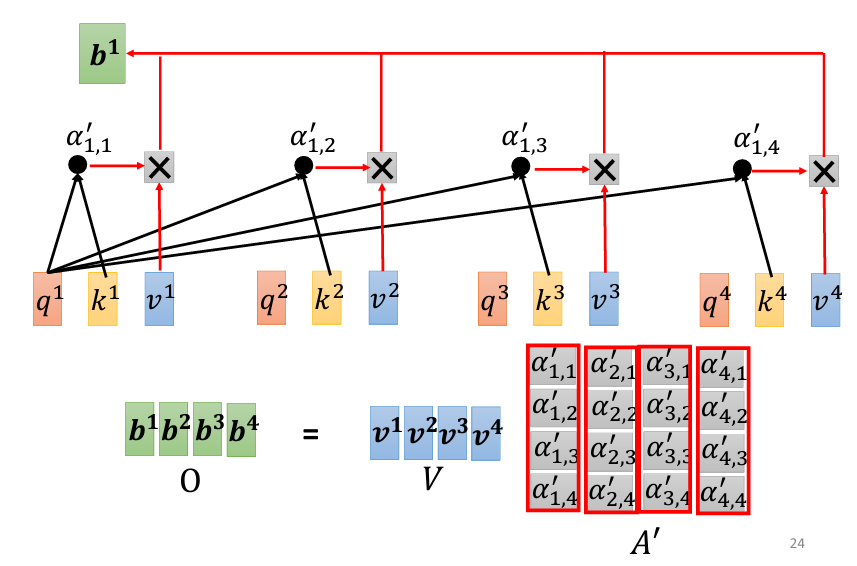
Self-Attention 操作的本質其實就是一系列矩陣運算,唯一需要學習的參數是三個權重矩陣 W_q、W_k、和 W_v。這三個矩陣是模型通過訓練數據來學習的,其他的操作如內積、轉置、正規化等則是已知且固定的。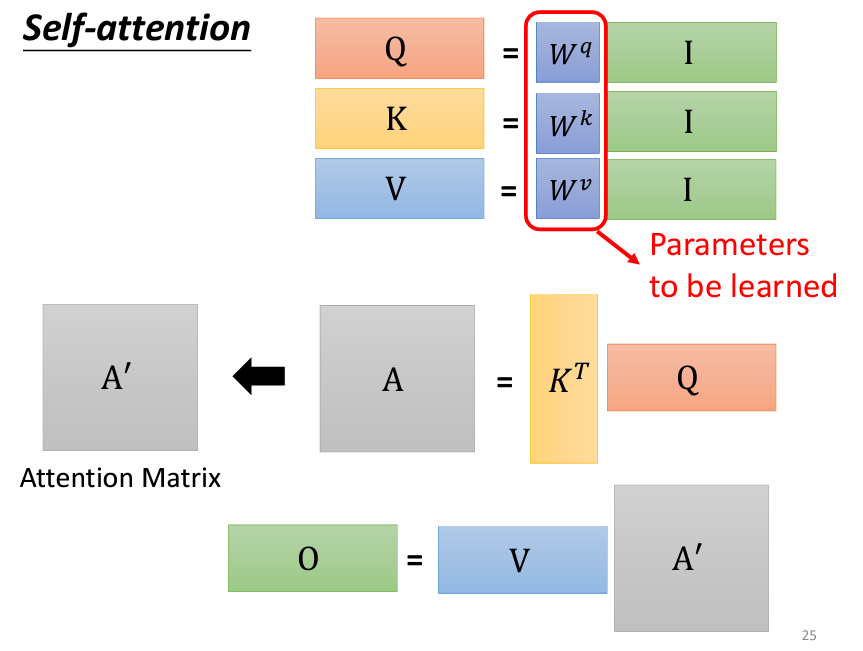
Self-Attention 的運作從輸入矩陣 I 到輸出矩陣 O 的流程可以視為:
I 生成 Q、K、V;Q 和 K 的相似度,得到 Attention Scores;V 進行加權求和,得到輸出 O。這一連串操作雖然有個很好聼的名字叫做注意力機制,但從實際的運算角度來說,只是一系列的矩陣乘法與正規化操作。
今天對於計算的講解就到這裏,明天會介紹Self-Attention更加進階的運算,如果篇幅允許的話,可能還會介紹Transformer這個模型。
以上的内容來自於臺大教授李宏毅:鏈接,我只是把他的影片寫成了筆記。
